import os
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '3'  # 设置日志级别为ERROR，以减少警告信息
# 禁用 Gemini 的底层库（gRPC 和 Abseil）在初始化日志警告
os.environ["GRPC_VERBOSITY"] = "ERROR"
os.environ["GLOG_minloglevel"] = "3"  # 0: INFO, 1: WARNING, 2: ERROR, 3: FATAL
os.environ["GLOG_minloglevel"] = "true"
import logging
import tensorflow as tf
tf.get_logger().setLevel(logging.ERROR)
tf.compat.v1.logging.set_verbosity(tf.compat.v1.logging.ERROR)
!export TF_FORCE_GPU_ALLOW_GROWTH=true
from pathlib import Path

temp_dir = Path(".temp")
temp_dir.mkdir(parents=True, exist_ok=True)

# Copyright 2018 The TensorFlow Authors.

#@title Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.

#@title MIT License
#
# Copyright (c) 2017 François Chollet
#
# Permission is hereby granted, free of charge, to any person obtaining a
# copy of this software and associated documentation files (the "Software"),
# to deal in the Software without restriction, including without limitation
# the rights to use, copy, modify, merge, publish, distribute, sublicense,
# and/or sell copies of the Software, and to permit persons to whom the
# Software is furnished to do so, subject to the following conditions:
#
# The above copyright notice and this permission notice shall be included in
# all copies or substantial portions of the Software.
#
# THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
# IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
# FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL
# THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
# LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING
# FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER
# DEALINGS IN THE SOFTWARE.

Basic regression: Predict fuel efficiency

在 TensorFlow.org上查看

在 Google Colab 中运行

在 GitHub 上查看源代码

下载笔记本

Note: 我们的 TensorFlow 社区翻译了这些文档。因为社区翻译是尽力而为， 所以无法保证它们是最准确的，并且反映了最新的 官方英文文档。如果您有改进此翻译的建议， 请提交 pull request 到 tensorflow/docs GitHub 仓库。要志愿地撰写或者审核译文，请加入 docs-zh-cn@tensorflow.org Google Group。

此教程使用经典的 Auto MPG 数据集并演示了如何构建模型来预测 20 世纪 70 年代末和 20 世纪 80 年代初汽车的燃油效率。为此，您需要为模型提供该时期的许多汽车的描述。这种描述包括诸如气缸、排量、马力和重量等特性。

此示例使用了 Keras API。（请访问 Keras 教程和指南以了解更多信息。）

# Use seaborn for pairplot.
!pip install -q seaborn

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns

# Make NumPy printouts easier to read.
np.set_printoptions(precision=3, suppress=True)

import tensorflow as tf

from tensorflow import keras
from tensorflow.keras import layers

print(tf.__version__)

2.17.0

Auto MPG 数据集

该数据集可以从 UCI机器学习库 中获取.

获取数据

首先下载数据集。

url = 'http://archive.ics.uci.edu/ml/machine-learning-databases/auto-mpg/auto-mpg.data'
column_names = ['MPG', 'Cylinders', 'Displacement', 'Horsepower', 'Weight',
                'Acceleration', 'Model Year', 'Origin']

raw_dataset = pd.read_csv(url, names=column_names,
                          na_values='?', comment='\t',
                          sep=' ', skipinitialspace=True)

dataset = raw_dataset.copy()
dataset.tail()

	MPG	Cylinders	Displacement	Horsepower	Weight	Acceleration	Model Year	Origin
393	27.0	4	140.0	86.0	2790.0	15.6	82	1
394	44.0	4	97.0	52.0	2130.0	24.6	82	2
395	32.0	4	135.0	84.0	2295.0	11.6	82	1
396	28.0	4	120.0	79.0	2625.0	18.6	82	1
397	31.0	4	119.0	82.0	2720.0	19.4	82	1

数据清洗

数据集包含一些未知值：

dataset.isna().sum()

MPG             0
Cylinders       0
Displacement    0
Horsepower      6
Weight          0
Acceleration    0
Model Year      0
Origin          0
dtype: int64

为了保证此初始教程简单，请删除这些行：

dataset = dataset.dropna()

"Origin" 列为分类数据，而不是数值数据。因此，下一步是使用 pd.get_dummies 对列中的值进行独热编码。

注：您可以设置 tf.keras.Model 来为您执行这种转换，但这超出了本教程的范围。有关示例，请参阅使用 Keras 预处理层对结构化数据进行分类或加载 CSV 数据教程。

dataset['Origin'] = dataset['Origin'].map({1: 'USA', 2: 'Europe', 3: 'Japan'})

dataset = pd.get_dummies(dataset, columns=['Origin'], prefix='', prefix_sep='', dtype="float32")
dataset.tail()

	MPG	Cylinders	Displacement	Horsepower	Weight	Acceleration	Model Year	Europe	Japan	USA
393	27.0	4	140.0	86.0	2790.0	15.6	82	0.0	0.0	1.0
394	44.0	4	97.0	52.0	2130.0	24.6	82	1.0	0.0	0.0
395	32.0	4	135.0	84.0	2295.0	11.6	82	0.0	0.0	1.0
396	28.0	4	120.0	79.0	2625.0	18.6	82	0.0	0.0	1.0
397	31.0	4	119.0	82.0	2720.0	19.4	82	0.0	0.0	1.0

将数据拆分为训练集和测试集

现在，将数据集拆分为训练集和测试集。您将在模型的最终评估中使用测试集。

train_dataset = dataset.sample(frac=0.8, random_state=0)
test_dataset = dataset.drop(train_dataset.index)

数据检查

检查训练集中几对列的联合分布。

第一行表明燃油效率 (MPG) 是所有其他参数的函数。其他行表示它们是彼此的函数。

sns.pairplot(train_dataset[['MPG', 'Cylinders', 'Displacement', 'Weight']], diag_kind='kde')

<seaborn.axisgrid.PairGrid at 0x7f2fb757cda0>

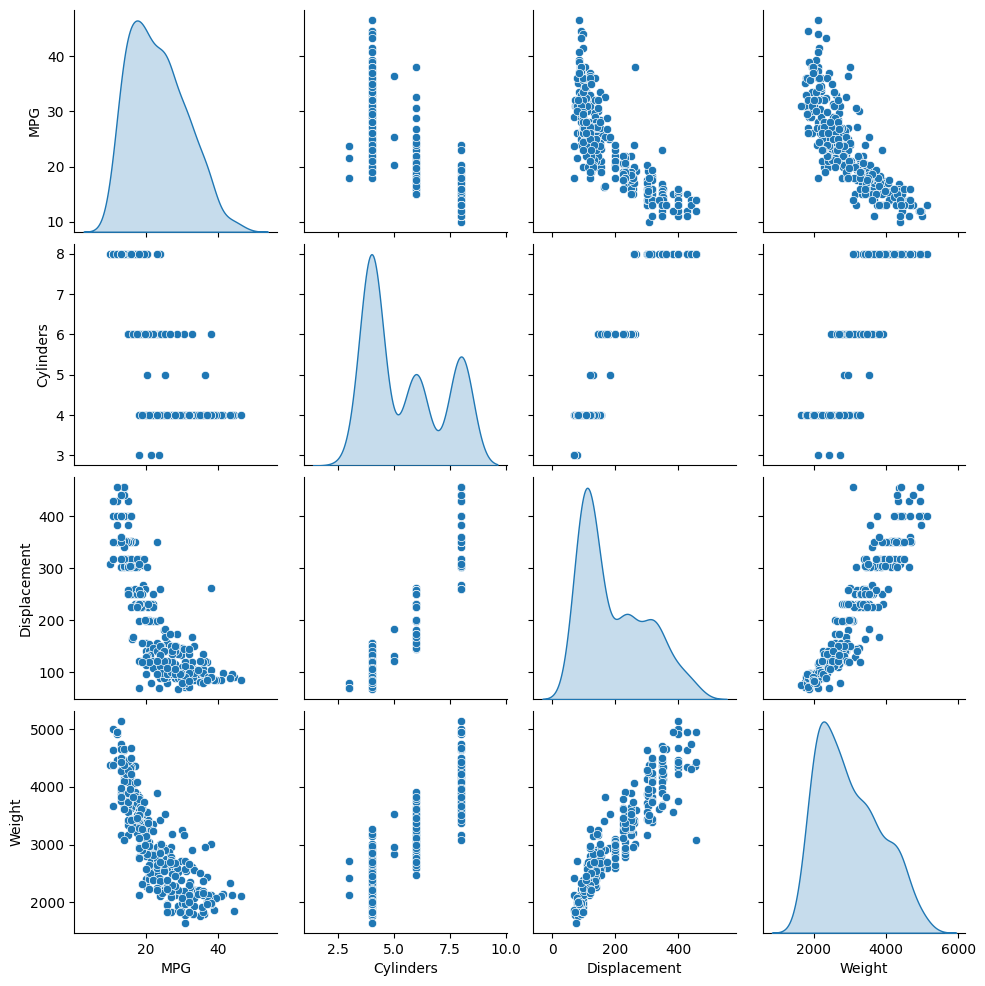
让我们也查看一下总体统计信息。请注意每个特征覆盖大为不同的范围：

train_dataset.describe().transpose()

	count	mean	std	min	25%	50%	75%	max
MPG	314.0	23.310510	7.728652	10.0	17.00	22.0	28.95	46.6
Cylinders	314.0	5.477707	1.699788	3.0	4.00	4.0	8.00	8.0
Displacement	314.0	195.318471	104.331589	68.0	105.50	151.0	265.75	455.0
Horsepower	314.0	104.869427	38.096214	46.0	76.25	94.5	128.00	225.0
Weight	314.0	2990.251592	843.898596	1649.0	2256.50	2822.5	3608.00	5140.0
Acceleration	314.0	15.559236	2.789230	8.0	13.80	15.5	17.20	24.8
Model Year	314.0	75.898089	3.675642	70.0	73.00	76.0	79.00	82.0
Europe	314.0	0.178344	0.383413	0.0	0.00	0.0	0.00	1.0
Japan	314.0	0.197452	0.398712	0.0	0.00	0.0	0.00	1.0
USA	314.0	0.624204	0.485101	0.0	0.00	1.0	1.00	1.0

从标签中分离特征

将目标值（“标签”）从特征中分离。此标签是您训练模型来预测的值。

train_features = train_dataset.copy()
test_features = test_dataset.copy()

train_labels = train_features.pop('MPG')
test_labels = test_features.pop('MPG')

归一化

在统计信息表中，可以很轻松地看到每个特征的范围的不同：

train_dataset.describe().transpose()[['mean', 'std']]

	mean	std
MPG	23.310510	7.728652
Cylinders	5.477707	1.699788
Displacement	195.318471	104.331589
Horsepower	104.869427	38.096214
Weight	2990.251592	843.898596
Acceleration	15.559236	2.789230
Model Year	75.898089	3.675642
Europe	0.178344	0.383413
Japan	0.197452	0.398712
USA	0.624204	0.485101

使用不同的尺度和范围对特征归一化是好的实践。尽管模型可能 在没有特征归一化的情况下收敛，它会使得模型训练更加复杂，并会造成生成的模型依赖输入所使用的单位选择。

归一化十分重要的一个原因是特征会与模型权重相乘。因此，输出尺度和梯度尺度受输入尺度的影响。

尽管模型可能在没有特征归一化的情况下收敛，但归一化会使训练更加稳定。

注：归一化独热特征没有任何好处，这里这样做是为了简单起见。有关如何使用预处理层的更多详细信息，请参阅使用预处理层指南和使用 Keras 预处理层对结构化数据进行分类教程。

归一化层

tf.keras.layers.Normalization 是一种将特征归一化添加到模型中的简洁且简单的方法。

第一步是创建层：

normalizer = tf.keras.layers.Normalization(axis=-1)

然后，通过调用 Normalization.adapt 以将预处理层的状态拟合到数据：

normalizer.adapt(np.array(train_features))

计算均值和方差，并将它们存储在层中。

print(normalizer.mean.numpy())

[[   5.478  195.318  104.869 2990.252   15.559   75.898    0.178    0.197
     0.624]]

当层被调用时，它会返回输入数据，每个特征将单独归一化：

train_features[:1]

	Cylinders	Displacement	Horsepower	Weight	Acceleration	Model Year	Europe	Japan	USA
146	4	90.0	75.0	2125.0	14.5	74	0.0	0.0	1.0

first = np.array(train_features[:1])

with np.printoptions(precision=2, suppress=True):
  print('First example:', first)
  print()
  print('Normalized:', normalizer(first).numpy())

First example: [[   4.    90.    75.  2125.    14.5   74.     0.     0.     1. ]]

Normalized: [[-0.87 -1.01 -0.79 -1.03 -0.38 -0.52 -0.47 -0.5   0.78]]

线性回归

在构建深度神经网络模型之前，首先使用一个和多个变量进行线性回归。

使用一个变量进行线性回归

从单变量线性回归开始，根据 'Horsepower' 预测 'MPG'。

使用 tf.keras 训练模型通常从定义模型架构开始。使用 tf.keras.Sequential 模型，它表示一系列步骤。

单变量线性回归模型有两个步骤：

• 使用 tf.keras.layers.Normalization 预处理层规一化 'Horsepower' 输入特征。

• 应用线性变换 (\(y = mx+b\)) 以使用线性层 (tf.keras.layers.Dense) 生成 1 个输出。

输入的数量可以由 input_shape 参数设置，也可以在模型第一次运行时自动设置。

首先，创建一个由 'Horsepower' 特征构成的 NumPy 数组。然后，实例化 tf.keras.layers.Normalization 并将其状态拟合到 horsepower 数据：

horsepower = np.array(train_features['Horsepower'])

horsepower_normalizer = layers.Normalization(axis=None)
horsepower_normalizer.adapt(horsepower)

构建 Keras 序贯模型：

horsepower_model = tf.keras.Sequential([
    layers.Input(shape=(1,)),
    horsepower_normalizer,
    layers.Dense(units=1)
])

horsepower_model.summary()

Model: "sequential"

┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓
┃ Layer (type)                    ┃ Output Shape           ┃       Param # ┃
┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩
│ normalization_1 (Normalization) │ (None, 1)              │             3 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ dense (Dense)                   │ (None, 1)              │             2 │
└─────────────────────────────────┴────────────────────────┴───────────────┘

 Total params: 5 (24.00 B)

 Trainable params: 2 (8.00 B)

 Non-trainable params: 3 (16.00 B)

此模型将根据 'Horsepower' 预测 'MPG'。

在前 10 个“马力”值上运行未经训练的模型。输出不会很好，但您会看到它具有预期的形状 (10, 1)：

horsepower_model.predict(horsepower[:10])

1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 160ms/step

WARNING: All log messages before absl::InitializeLog() is called are written to STDERR
I0000 00:00:1729738825.939939 3280987 service.cc:146] XLA service 0x7f2c40004cf0 initialized for platform CUDA (this does not guarantee that XLA will be used). Devices:
I0000 00:00:1729738825.939973 3280987 service.cc:154]   StreamExecutor device (0): NVIDIA GeForce RTX 3090, Compute Capability 8.6
I0000 00:00:1729738825.939981 3280987 service.cc:154]   StreamExecutor device (1): NVIDIA GeForce RTX 2080 Ti, Compute Capability 7.5
I0000 00:00:1729738826.047359 3280987 device_compiler.h:188] Compiled cluster using XLA!  This line is logged at most once for the lifetime of the process.

array([[-0.019],
       [-0.011],
       [ 0.035],
       [-0.026],
       [-0.024],
       [-0.009],
       [-0.028],
       [-0.024],
       [-0.006],
       [-0.011]], dtype=float32)

构建模型后，使用 Keras Model.compile 方法配置训练过程。要编译的最重要参数是 loss 和 optimizer，因为它们定义了将要优化的内容 (mean_absolute_error) 以及优化的方法（使用 tf.keras.optimizers.Adam）。

horsepower_model.compile(
    optimizer=tf.keras.optimizers.Adam(learning_rate=0.1),
    loss='mean_absolute_error')

使用 Keras Model.fit 执行 100 个周期的训练：

%%time
history = horsepower_model.fit(
    train_features['Horsepower'],
    train_labels,
    epochs=100,
    # Suppress logging.
    verbose=0,
    # Calculate validation results on 20% of the training data.
    validation_split = 0.2)

CPU times: user 7.16 s, sys: 1.3 s, total: 8.46 s
Wall time: 6.55 s

使用 history 对象中存储的统计信息呈现模型的训练进度：

hist = pd.DataFrame(history.history)
hist['epoch'] = history.epoch
hist.tail()

	loss	val_loss	epoch
95	3.801883	4.189487	95
96	3.802329	4.193586	96
97	3.804766	4.193433	97
98	3.804802	4.180914	98
99	3.803075	4.195196	99

def plot_loss(history):
  plt.plot(history.history['loss'], label='loss')
  plt.plot(history.history['val_loss'], label='val_loss')
  plt.ylim([0, 10])
  plt.xlabel('Epoch')
  plt.ylabel('Error [MPG]')
  plt.legend()
  plt.grid(True)

plot_loss(history)

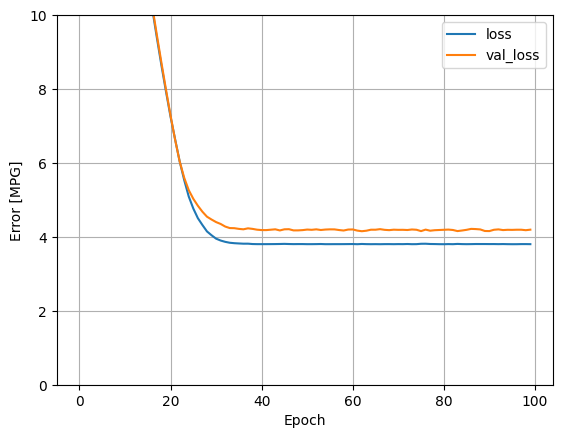
收集测试集上的结果，供后面使用：

test_results = {}

test_results['horsepower_model'] = horsepower_model.evaluate(
    test_features['Horsepower'],
    test_labels, verbose=0)

由于这是一个单变量回归，很容易将模型的预测视为输入的函数：

x = tf.linspace(0.0, 250, 251)
y = horsepower_model.predict(x)

8/8 ━━━━━━━━━━━━━━━━━━━━ 0s 18ms/step

def plot_horsepower(x, y):
  plt.scatter(train_features['Horsepower'], train_labels, label='Data')
  plt.plot(x, y, color='k', label='Predictions')
  plt.xlabel('Horsepower')
  plt.ylabel('MPG')
  plt.legend()

plot_horsepower(x, y)

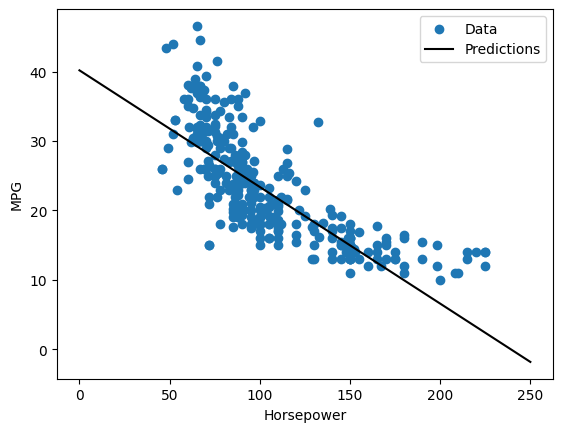
使用多个输入进行线性回归

您可以使用几乎相同的设置根据多个输入进行预测。此模型仍然执行相同的 \(y = mx+b\)，只是 \(m\) 是一个矩阵，而 \(b\) 是一个向量。

再次创建一个两步 Keras 序贯模型，第一层为您之前定义并拟合到整个数据集的 normalizer (tf.keras.layers.Normalization(axis=-1))：

linear_model = tf.keras.Sequential([
    normalizer,
    layers.Dense(units=1)
])

当您对一批输入调用 Model.predict 时，它会为每个样本生成 units=1 输出。

linear_model.predict(train_features[:10])

1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 200ms/step

array([[-1.12 ],
       [-0.624],
       [ 1.936],
       [-2.406],
       [-0.512],
       [ 0.408],
       [-0.474],
       [ 0.402],
       [ 0.685],
       [ 0.963]], dtype=float32)

当您调用模型时，将构建其权重矩阵 – 可以看到 kernel 权重（\(y=mx+b\) 中的 \(m\)）的形状为 (9, 1)：

linear_model.layers[1].kernel

<KerasVariable shape=(9, 1), dtype=float32, path=sequential_1/dense_1/kernel>

使用 Keras Model.compile 配置模型并使用 Model.fit 训练 100 个周期：

linear_model.compile(
    optimizer=tf.keras.optimizers.Adam(learning_rate=0.1),
    loss='mean_absolute_error')

%%time
history = linear_model.fit(
    train_features,
    train_labels,
    epochs=100,
    # Suppress logging.
    verbose=0,
    # Calculate validation results on 20% of the training data.
    validation_split = 0.2)

CPU times: user 7.04 s, sys: 1.22 s, total: 8.25 s
Wall time: 6.44 s

使用此回归模型中的所有输入可以实现比 horsepower_model（具有一个输入）低得多的训练和验证误差：

plot_loss(history)

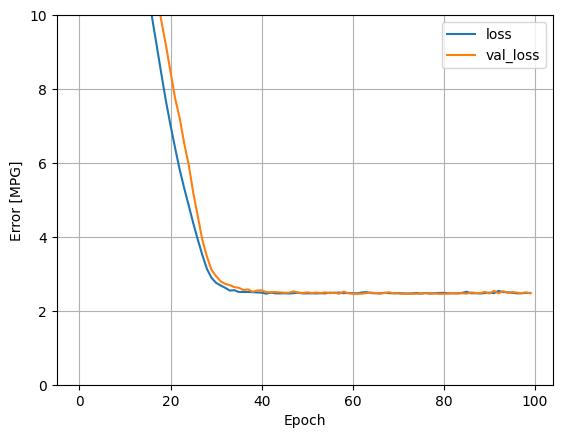
收集测试集上的结果，供后面使用：

test_results['linear_model'] = linear_model.evaluate(
    test_features, test_labels, verbose=0)

使用深度神经网络 (DNN) 进行回归

在上一部分中，您为单输入和多输入实现了两个线性模型。

在此，您将实现单输入和多输入 DNN 模型。

除了将模型扩展为包括一些“隐藏”非线性层之外，代码基本相同。此处的名称“隐藏”仅表示不直接连接到输入或输出。

这些模型包含的层比线性模型多一些：

• 归一化层和以前一样（对于单输入模型使用 horsepower_normalizer，对于多输入模型使用 normalizer）。

• 使用 ReLU (relu) 激活函数非线性的两个隐藏非线性 Dense 层。

• 一个线性 Dense 单输出层。

两个模型都将使用相同的训练过程，因此 compile 方法包含在下面的 build_and_compile_model 函数中。

def build_and_compile_model(norm):
  model = keras.Sequential([
      norm,
      layers.Dense(64, activation='relu'),
      layers.Dense(64, activation='relu'),
      layers.Dense(1)
  ])

  model.compile(loss='mean_absolute_error',
                optimizer=tf.keras.optimizers.Adam(0.001))
  return model

使用 DNN 和单输入进行回归

创建一个 DNN 模型，仅将 'Horsepower' 作为输入，将 'Horsepower'（之前定义）作为归一化层：

dnn_horsepower_model = build_and_compile_model(horsepower_normalizer)

此模型比线性模型的可训练参数多很多。

dnn_horsepower_model.summary()

Model: "sequential_2"

┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓
┃ Layer (type)                    ┃ Output Shape           ┃       Param # ┃
┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩
│ normalization_1 (Normalization) │ (None, 1)              │             3 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ dense_2 (Dense)                 │ ?                      │   0 (unbuilt) │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ dense_3 (Dense)                 │ ?                      │   0 (unbuilt) │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ dense_4 (Dense)                 │ ?                      │   0 (unbuilt) │
└─────────────────────────────────┴────────────────────────┴───────────────┘

 Total params: 3 (16.00 B)

 Trainable params: 0 (0.00 B)

 Non-trainable params: 3 (16.00 B)

使用 Keras Model.fit 训练模型：

%%time
history = dnn_horsepower_model.fit(
    train_features['Horsepower'],
    train_labels,
    validation_split=0.2,
    verbose=0, epochs=100)

CPU times: user 18.3 s, sys: 1.67 s, total: 19.9 s
Wall time: 9.41 s

此模型略优于线性单输入 horsepower_model：

plot_loss(history)

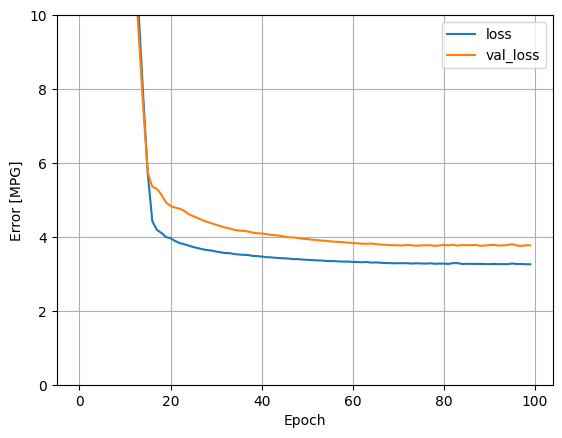
如果您将预测值绘制为 'Horsepower' 的函数，应看到此模型如何利用隐藏层提供的非线性：

x = tf.linspace(0.0, 250, 251)
y = dnn_horsepower_model.predict(x)

8/8 ━━━━━━━━━━━━━━━━━━━━ 1s 48ms/step

plot_horsepower(x, y)

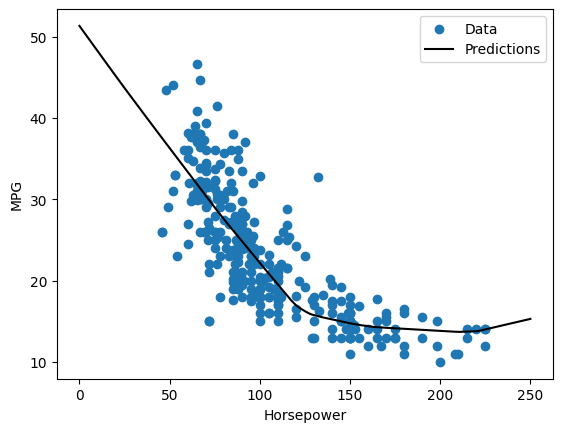
收集测试集上的结果，供后面使用：

test_results['dnn_horsepower_model'] = dnn_horsepower_model.evaluate(
    test_features['Horsepower'], test_labels,
    verbose=0)

使用 DNN 和多输入进行回归

使用所有输入重复前面的过程。模型的性能在验证数据集上会略有提高。

dnn_model = build_and_compile_model(normalizer)
dnn_model.summary()

Model: "sequential_3"

┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓
┃ Layer (type)                    ┃ Output Shape           ┃       Param # ┃
┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩
│ normalization (Normalization)   │ (10, 9)                │            19 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ dense_5 (Dense)                 │ ?                      │   0 (unbuilt) │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ dense_6 (Dense)                 │ ?                      │   0 (unbuilt) │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ dense_7 (Dense)                 │ ?                      │   0 (unbuilt) │
└─────────────────────────────────┴────────────────────────┴───────────────┘

 Total params: 19 (80.00 B)

 Trainable params: 0 (0.00 B)

 Non-trainable params: 19 (80.00 B)

%%time
history = dnn_model.fit(
    train_features,
    train_labels,
    validation_split=0.2,
    verbose=0, epochs=100)

CPU times: user 9.77 s, sys: 1.29 s, total: 11.1 s
Wall time: 8.31 s

plot_loss(history)

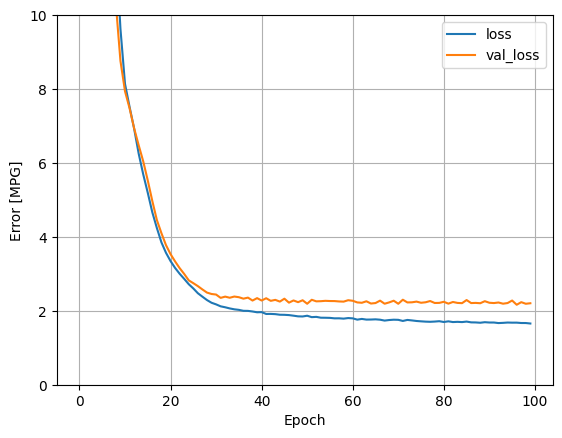
收集测试集上的结果：

test_results['dnn_model'] = dnn_model.evaluate(test_features, test_labels, verbose=0)

性能

所有模型都已经过训练，因此您可以查看它们的测试集性能：

pd.DataFrame(test_results, index=['Mean absolute error [MPG]']).T

	Mean absolute error [MPG]
horsepower_model	3.646849
linear_model	2.500054
dnn_horsepower_model	2.905027
dnn_model	1.643063

这些结果与训练期间看到的验证误差相匹配。

做预测

您现在可以使用 Keras Model.predict，在测试集上利用 dnn_model 进行预测并查看损失：

test_predictions = dnn_model.predict(test_features).flatten()

a = plt.axes(aspect='equal')
plt.scatter(test_labels, test_predictions)
plt.xlabel('True Values [MPG]')
plt.ylabel('Predictions [MPG]')
lims = [0, 50]
plt.xlim(lims)
plt.ylim(lims)
_ = plt.plot(lims, lims)

3/3 ━━━━━━━━━━━━━━━━━━━━ 1s 175ms/step

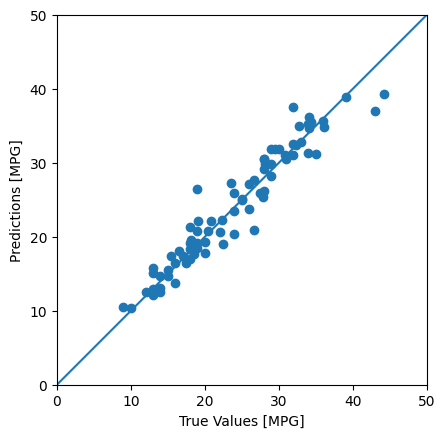
看起来模型预测得相当出色。

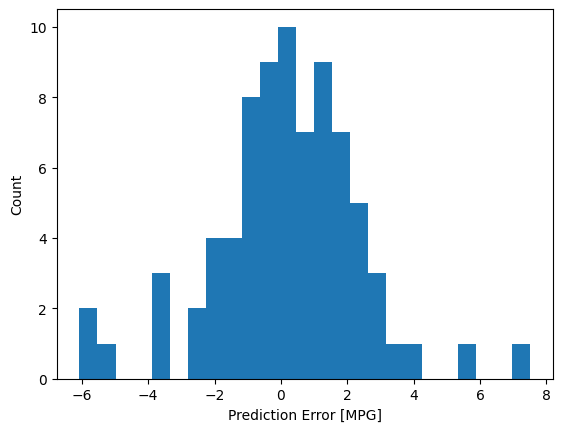
现在，查看一下误差分布：

error = test_predictions - test_labels
plt.hist(error, bins=25)
plt.xlabel('Prediction Error [MPG]')
_ = plt.ylabel('Count')

如果您对模型感到满意，请使用 Model.save 将其保存以备后续使用：

dnn_model.save(temp_dir/'dnn_model.keras')

如果您重新加载模型，它会给出相同的输出：

reloaded = tf.keras.models.load_model(temp_dir/'dnn_model.keras')

test_results['reloaded'] = reloaded.evaluate(
    test_features, test_labels, verbose=0)

pd.DataFrame(test_results, index=['Mean absolute error [MPG]']).T

	Mean absolute error [MPG]
horsepower_model	3.646849
linear_model	2.500054
dnn_horsepower_model	2.905027
dnn_model	1.643063
reloaded	1.643063

结论

本笔记本 (notebook) 介绍了一些处理回归问题的技术。

• 均方误差 (MSE) (tf.keras.losses.MeanSquaredError) 和平均绝对误差 (MAE) (tf.keras.losses.MeanAbsoluteError) 是用于回归问题的常见损失函数。MAE 对异常值不那么敏感。不同的损失函数用于分类问题。

• 类似的，用于回归的评估指标与分类不同。 常见的回归指标是平均绝对误差（MAE）。

• 当数字输入数据特征的值存在不同范围时，每个特征应独立缩放到相同范围。

• 过拟合是 DNN 模型的常见问题，但本教程不存在此问题。有关这方面的更多帮助，请访问过拟合和欠拟合教程。