##### Copyright 2023 The TF-Agents Authors.
#@title Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
RL 和深度 Q 网络简介#
 在 TensorFlow.org 上查看 在 TensorFlow.org 上查看 |
 在 Google Colab 运行 在 Google Colab 运行 |
 在 Github 上查看源代码 在 Github 上查看源代码 |
 下载笔记本 下载笔记本 |
简介#
强化学习 (RL) 是一种通用框架,其中代理可以学习在所处的环境中执行操作来使奖励最大化。两个主要组件是环境(代表要解决的问题)和代理(代表学习算法)。
代理与环境持续相互作用。在每个时间步骤,代理都会根据其策略 \(\pi(a_t|s_t)\)(其中 \(s_t\) 是来自环境的当前观测值)对环境执行操作并获得奖励 \(r_{t+1}\) 和来自环境的下一个观测值 \(s_{t+1}\)。目标是改进策略,使奖励总和(回报)最大化。
注:区分环境的 state 和 observation 非常重要,这是代理可以看到的环境 state 部分,例如在扑克游戏中,环境状态由属于所有玩家的纸牌和公共牌组成,但是代理只能观测到自己的纸牌和部分公共牌。在大多数文献中,这些术语可互换使用,观测值也表示为 \(s\)。
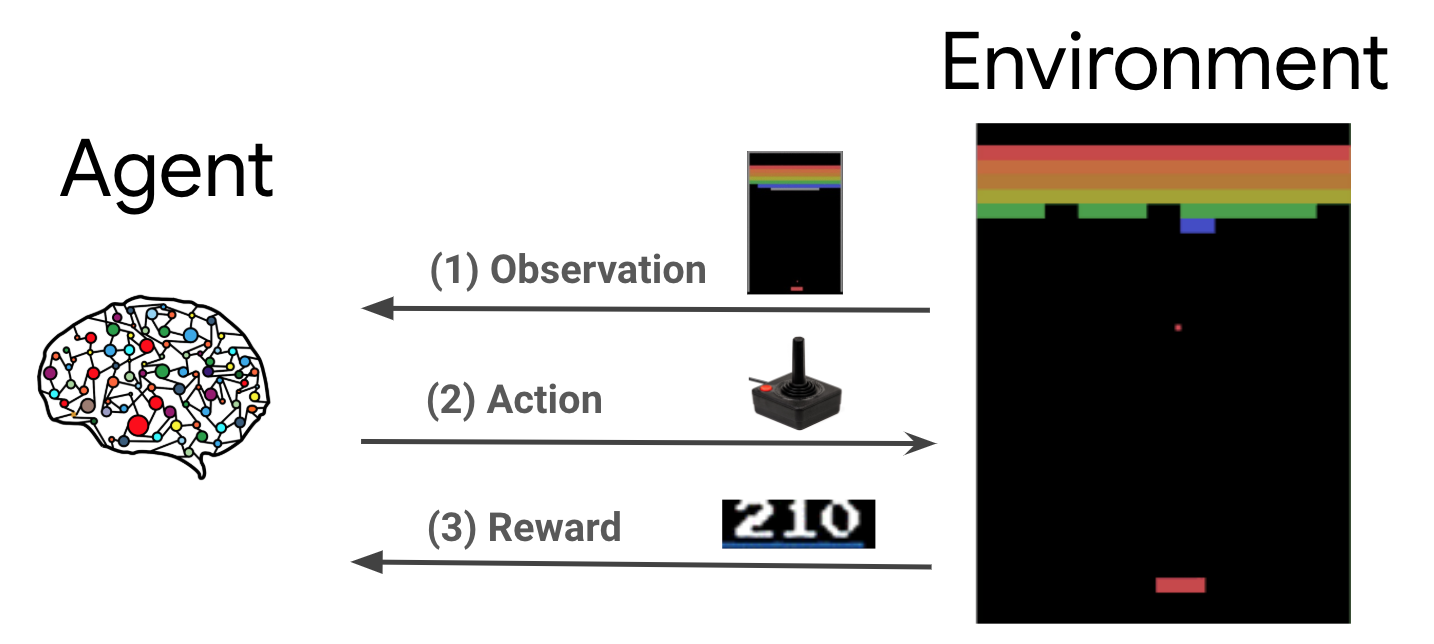
这是非常通用的框架,可以对游戏、机器人等各种顺序决策问题进行建模。
Cartpole 环境#
Cartpole 环境是最著名的经典强化学习问题之一(RL 的 “Hello, World!”)。一根长杆连接到一个小车上,小车可以沿着无摩擦的轨道移动。长杆开始时是直立的,目标是通过控制小车来防止其倒下。
来自环境 \(s_t\) 的观测值是一个 4D 向量,表示小车的位置和速度以及长杆的角度和角速度。
代理可以通过执行以下两个操作 \(a_t\) 之一来控制系统:向右 (+1) 或向左 (-1) 推小车。
对于长杆保持直立的每个时间步骤,都会提供 \(r_{t+1} = 1\) 奖励。如果满足以下任一条件,则片段结束:
长杆超过某个角度限制
小车移出世界边缘
经过 200 个时间步骤。
代理的目标是学习策略 \(\pi(a_t|s_t)\),以使片段 \(\sum_{t=0}^{T} \gamma^t r_t\) 中的奖励总和最大化。在这里,\(\gamma\) 是以 \([0, 1]\) 表示的折扣因子,该因子相对于即时奖励对未来的奖励打折扣。此参数有助于我们专注于策略,使其更关心快速获得奖励。
DQN 代理#
DQN(深度 Q 网络)算法由 DeepMind 在 2015 年开发。通过将强化学习和深度神经网络进行大规模组合,它能够通关各种 Atari 游戏(有些甚至达到了超出人类能力的水平)。此算法通过使用深度神经网络和一种称为经验回放的技术来增强经典的 RL 算法(称为 Q-Learning)开发而成。
Q-Learning#
Q-Learning 基于 Q 函数的概念。策略 \(\pi\), \(Q^{\pi}(s, a)\) 的 Q 函数(又称状态-操作值函数)用于衡量通过首先采取操作 \(a\)、随后采取策略 \(\pi\),从状态 \(s\) 获得的预期回报或折扣奖励总和。我们将最优 Q 函数 \(Q^*(s, a)\) 定义为从观测值 \(s\) 开始,先采取操作 \(a\),随后采取最优策略所能获得的最大回报。最优 Q 函数遵循以下贝尔曼最优性方程:
$\begin{equation}Q^\ast(s, a) = \mathbb{E}[ r + \gamma \max_{a'} Q^\ast(s', a') ]\end{equation}$
这意味着,从状态 \(s\) 和操作 \(a\) 获得的最大回报等于即时奖励 \(r\) 与通过遵循最优策略,随后直到片段结束所获得的回报(折扣因子为 \(\gamma\))的总和(即,来自下一个状态 \(s'\) 的最高奖励)。期望是在即时奖励 \(r\) 的分布以及可能的下一个状态 \(s'\) 的基础上计算的。
Q-Learning 背后的基本思想是使用贝尔曼最优性方程作为迭代更新 \(Q_{i+1}(s, a) \leftarrow \mathbb{E}\left[ r + \gamma \max_{a'} Q_{i}(s', a')\right]\),可以表明它会收敛到最优 \(Q\) 函数,即 \(Q_i \rightarrow Q^*\) 作为 \(i \rightarrow \infty\)(请参阅 DQN 论文)。
深度 Q-Learning#
对于大多数问题,将 \(Q\) 函数表示为包含 \(s\) 和 \(a\) 每种组合的值的表是不切实际的。相反,我们训练一个函数逼近器(例如,带参数 \(\theta\) 的神经网络)来估算 Q 值,即 \(Q(s, a; \theta) \approx Q^*(s, a)\)。这可以通过在每个步骤 \(i\) 使以下损失最小化来实现:
\(\begin{equation}L_i(\theta_i) = \mathbb{E}{em0}{s, a, r, s'\sim \rho(.)} \left[ (y_i - Q(s, a; \theta_i))^2 \right]\end{equation}\),其中 \(y_i = r + \gamma \max{/em0}{a'} Q(s', a'; \theta_{i-1})\)
此处,\(y_i\) is 称为 TD(时间差分)目标,而 \(y_i - Q\) 称为 TD 误差。\(\rho\) 表示行为分布,即从环境中收集的转换 \({s, a, r, s'}\) 的分布。
注意,先前迭代 \(\theta_{i-1}\) 中的参数是固定的,不会更新。实际上,我们使用前几次迭代而不是最后一次迭代的网络参数快照。此副本称为目标网络。
Q-Learning 是一种离策略算法,可在学习贪心策略 \(a = \max_{a} Q(s, a; \theta)\) 的同时使用不同的行为策略在环境/收集数据过程中执行操作。此行为策略通常是一种 \(\epsilon\) 贪心策略,可选择概率为 \(1-\epsilon\) 的贪心操作和概率为 \(\epsilon\) 的随机操作,以确保良好覆盖状态-操作空间。
经验回放#
为了避免计算 DQN 损失的全期望,我们可以使用随机梯度下降算法将其最小化。如果仅使用最后的转换 \({s, a, r, s'}\) 计算损失,这将简化为标准 Q-Learning。
Atari DQN 工作引入了一种称为“经验回放”的技术,可使网络更新更加稳定。在数据收集的每个时间步骤,转换都会添加到称为回放缓冲区的循环缓冲区中。然后,在训练过程中,我们不是仅仅使用最新的转换来计算损失及其梯度,而是使用从回放缓冲区中采样的转换的 mini-batch 来计算它们。这样做有两个优点:通过在许多更新中重用每个转换来提高数据效率,以及在批次中使用不相关的转换来提高稳定性。
TF-Agents 中基于 Cartpole 的 DQN#
TF-Agents 提供了训练 DQN 代理所需的全部组件,例如代理本身、环境、策略、网络、回放缓冲区、数据收集循环和指标。这些组件以 Python 函数或 TensorFlow 计算图运算的形式实现,我们还提供用于在它们之间进行转换的包装器。此外,TF-Agents 还支持 TensorFlow 2.0 模式,这样我们便能在命令式模式下使用 TF。


