高级自动微分#
 在 TensorFlow.org 上查看 在 TensorFlow.org 上查看 |
 在 Google Colab 中运行 在 Google Colab 中运行
|
 在 GitHub 上查看源代码 在 GitHub 上查看源代码 |
 下载笔记本 下载笔记本 |
梯度和自动微分简介指南包括在 TensorFlow 中计算梯度所需的全部内容。本指南重点介绍 tf.GradientTape API 更深入、更不常见的功能。
设置#
from set_env import temp_dir
import tensorflow as tf
import matplotlib as mpl
import matplotlib.pyplot as plt
mpl.rcParams['figure.figsize'] = (8, 6)
控制梯度记录#
在自动微分指南中,您已了解构建梯度计算时如何控制条带监视变量和张量。
条带还具有操作记录的方法。
停止记录#
如果您希望停止记录梯度,可以使用 tf.GradientTape.stop_recording 暂时挂起记录。
如果您不希望在模型中间对复杂运算微分,这可能有助于减少开销。其中可能包括计算指标或中间结果:
x = tf.Variable(2.0)
y = tf.Variable(3.0)
with tf.GradientTape() as t:
x_sq = x * x
with t.stop_recording():
y_sq = y * y
z = x_sq + y_sq
grad = t.gradient(z, {'x': x, 'y': y})
print('dz/dx:', grad['x']) # 2*x => 4
print('dz/dy:', grad['y'])
dz/dx: tf.Tensor(4.0, shape=(), dtype=float32)
dz/dy: None
重置/从头开始纪录#
如果您希望完全重新开始,请使用 tf.GradientTape.reset。通常,直接退出梯度带块并重新开始比较易于读取,但在退出梯度带块有困难或不可行时,可以使用 reset 方法。
x = tf.Variable(2.0)
y = tf.Variable(3.0)
reset = True
with tf.GradientTape() as t:
y_sq = y * y
if reset:
# Throw out all the tape recorded so far.
t.reset()
z = x * x + y_sq
grad = t.gradient(z, {'x': x, 'y': y})
print('dz/dx:', grad['x']) # 2*x => 4
print('dz/dy:', grad['y'])
dz/dx: tf.Tensor(4.0, shape=(), dtype=float32)
dz/dy: None
精确停止梯度流#
与上面的全局条带控制相比,tf.stop_gradient 函数更加精确。它可以用来阻止梯度沿着特定路径流动,而不需要访问条带本身:
x = tf.Variable(2.0)
y = tf.Variable(3.0)
with tf.GradientTape() as t:
y_sq = y**2
z = x**2 + tf.stop_gradient(y_sq)
grad = t.gradient(z, {'x': x, 'y': y})
print('dz/dx:', grad['x']) # 2*x => 4
print('dz/dy:', grad['y'])
dz/dx: tf.Tensor(4.0, shape=(), dtype=float32)
dz/dy: None
自定义梯度#
在某些情况下,您可能需要精确控制梯度的计算方式,而不是使用默认值。这些情况包括:
正在编写的新运算没有定义的梯度。
默认计算在数值上不稳定。
您希望从前向传递缓存开销大的计算。
您想修改一个值(例如,使用
tf.clip_by_value或tf.math.round)而不修改梯度。
对于第一种情况,要编写新运算,您可以使用 tf.RegisterGradient 自行设置。(请参阅 API 文档了解详细信息)。(注意,梯度注册为全局,需谨慎更改。)
对于后三种情况,可以使用 tf.custom_gradient。
以下示例将 tf.clip_by_norm 应用于中间梯度:
# Establish an identity operation, but clip during the gradient pass.
@tf.custom_gradient
def clip_gradients(y):
def backward(dy):
return tf.clip_by_norm(dy, 0.5)
return y, backward
v = tf.Variable(2.0)
with tf.GradientTape() as t:
output = clip_gradients(v * v)
print(t.gradient(output, v)) # calls "backward", which clips 4 to 2
tf.Tensor(2.0, shape=(), dtype=float32)
请参阅 tf.custom_gradient 装饰器 API 文档,了解更多详细信息。
SavedModel 中的自定义梯度#
注:此功能将从 TensorFlow 2.6 开始提供。
可以使用选项 tf.saved_model.SaveOptions(experimental_custom_gradients=True) 将自定义梯度保存到 SavedModel。
要保存到 SavedModel,梯度函数必须可以跟踪(要了解详情,请参阅使用 tf.function 提高性能指南)。
class MyModule(tf.Module):
@tf.function(input_signature=[tf.TensorSpec(None)])
def call_custom_grad(self, x):
return clip_gradients(x)
model = MyModule()
tf.saved_model.save(
model,
temp_dir/'saved_model',
options=tf.saved_model.SaveOptions(experimental_custom_gradients=True))
# The loaded gradients will be the same as the above example.
v = tf.Variable(2.0)
loaded = tf.saved_model.load(temp_dir/'saved_model')
with tf.GradientTape() as t:
output = loaded.call_custom_grad(v * v)
print(t.gradient(output, v))
tf.Tensor(2.0, shape=(), dtype=float32)
关于上述示例的注意事项:如果您尝试用 tf.saved_model.SaveOptions(experimental_custom_gradients=False) 替换上面的代码,梯度仍会在加载时产生相同的结果。原因在于,梯度注册表仍然包含函数 call_custom_op 中使用的自定义梯度。但是,如果在没有自定义梯度的情况下保存后重新启动运行时,则在 tf.GradientTape 下运行加载的模型会抛出错误:LookupError: No gradient defined for operation 'IdentityN' (op type: IdentityN)。
多个条带#
多个条带无缝交互。
例如,下面每个条带监视不同的张量集:
x0 = tf.constant(0.0)
x1 = tf.constant(0.0)
with tf.GradientTape() as tape0, tf.GradientTape() as tape1:
tape0.watch(x0)
tape1.watch(x1)
y0 = tf.math.sin(x0)
y1 = tf.nn.sigmoid(x1)
y = y0 + y1
ys = tf.reduce_sum(y)
tape0.gradient(ys, x0).numpy() # cos(x) => 1.0
1.0
tape1.gradient(ys, x1).numpy() # sigmoid(x1)*(1-sigmoid(x1)) => 0.25
0.25
高阶梯度#
tf.GradientTape 上下文管理器内的运算会被记录下来,以供自动微分。如果在该上下文中计算梯度,梯度计算也会被记录。因此,完全相同的 API 也适用于高阶梯度。
例如:
x = tf.Variable(1.0) # Create a Tensorflow variable initialized to 1.0
with tf.GradientTape() as t2:
with tf.GradientTape() as t1:
y = x * x * x
# Compute the gradient inside the outer `t2` context manager
# which means the gradient computation is differentiable as well.
dy_dx = t1.gradient(y, x)
d2y_dx2 = t2.gradient(dy_dx, x)
print('dy_dx:', dy_dx.numpy()) # 3 * x**2 => 3.0
print('d2y_dx2:', d2y_dx2.numpy()) # 6 * x => 6.0
dy_dx: 3.0
d2y_dx2: 6.0
虽然这确实可以得到标量函数的二次导数,但这种模式并不能通用于生成黑塞矩阵,因为 tf.GradientTape.gradient 只计算标量的梯度。要构造黑塞矩阵,请参见“雅可比矩阵”部分下的“黑塞矩阵”示例。
当您从梯度计算标量,然后产生的标量作为第二个梯度计算的源时,“嵌套调用 tf.GradientTape.gradient”是一种不错的模式,如以下示例所示。
示例:输入梯度正则化#
许多模型都容易受到“对抗样本”影响。这种技术的集合会修改模型的输入,进而混淆模型输出。最简单的实现(例如,使用 Fast Gradient Signed Method 攻击的对抗样本)沿着输出相对于输入的梯度(即“输入梯度”) 迈出一步。
一种增强相对于对抗样本的稳健性的方法是输入梯度正则化(Finlay 和 Oberman,2019 年),这种方法会尝试将输入梯度的幅度最小化。如果输入梯度较小,那么输出的变化也应该较小。
以下是输入梯度正则化的简单实现:
使用内条带计算输出相对于输入的梯度。
计算该输入梯度的幅度。
计算该幅度相对于模型的梯度。
x = tf.random.normal([7, 5])
layer = tf.keras.layers.Dense(10, activation=tf.nn.relu)
with tf.GradientTape() as t2:
# The inner tape only takes the gradient with respect to the input,
# not the variables.
with tf.GradientTape(watch_accessed_variables=False) as t1:
t1.watch(x)
y = layer(x)
out = tf.reduce_sum(layer(x)**2)
# 1. Calculate the input gradient.
g1 = t1.gradient(out, x)
# 2. Calculate the magnitude of the input gradient.
g1_mag = tf.norm(g1)
# 3. Calculate the gradient of the magnitude with respect to the model.
dg1_mag = t2.gradient(g1_mag, layer.trainable_variables)
[var.shape for var in dg1_mag]
[TensorShape([5, 10]), TensorShape([10])]
雅可比矩阵#
以上所有示例都取标量目标相对于某些源张量的梯度。
雅可比矩阵代表向量值函数的梯度。每行都包含其中一个向量元素的梯度。
tf.GradientTape.jacobian 方法让您能够有效计算雅可比矩阵。
注意:
类似于
gradient:sources参数可以是张量或张量的容器。不同于
gradient:target张量必须是单个张量。
标量源#
作为第一个示例,以下是矢量目标相对于标量源的雅可比矩阵。
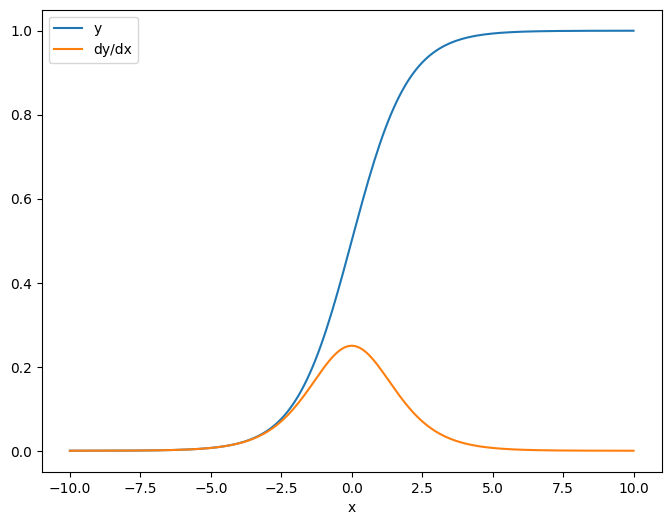
x = tf.linspace(-10.0, 10.0, 200+1)
delta = tf.Variable(0.0)
with tf.GradientTape() as tape:
y = tf.nn.sigmoid(x+delta)
dy_dx = tape.jacobian(y, delta)
当您相对于标量取雅可比矩阵时,结果为目标的形状,并给出每个元素相对于源的梯度:
print(y.shape)
print(dy_dx.shape)
(201,)
(201,)
plt.plot(x.numpy(), y, label='y')
plt.plot(x.numpy(), dy_dx, label='dy/dx')
plt.legend()
_ = plt.xlabel('x')
张量源#
无论输入是标量还是张量,tf.GradientTape.jacobian 都能有效计算源的每个元素相对于目标的每个元素的梯度。
例如,此层的输出的形状为 (10,7)。
x = tf.random.normal([7, 5])
layer = tf.keras.layers.Dense(10, activation=tf.nn.relu)
with tf.GradientTape(persistent=True) as tape:
y = layer(x)
y.shape
TensorShape([7, 10])
层内核的形状是 (5,10)。
layer.kernel.shape
TensorShape([5, 10])
将这两个形状连在一起就是输出相对于内核的雅可比矩阵的形状:
j = tape.jacobian(y, layer.kernel)
j.shape
TensorShape([7, 10, 5, 10])
如果您在目标的维度上求和,会得到由 tf.GradientTape.gradient 计算的总和的梯度:
g = tape.gradient(y, layer.kernel)
print('g.shape:', g.shape)
j_sum = tf.reduce_sum(j, axis=[0, 1])
delta = tf.reduce_max(abs(g - j_sum)).numpy()
assert delta < 1e-3
print('delta:', delta)
g.shape: (5, 10)
delta: 4.7683716e-07
示例:黑塞矩阵#
虽然 tf.GradientTape 并没有给出构造黑塞矩阵的显式方法,但可以使用 tf.GradientTape.jacobian 方法进行构建。
注:黑塞矩阵包含 N**2 个参数。由于这个原因和其他原因,它对于大多数模型都不实际。此示例主要是为了演示如何使用 tf.GradientTape.jacobian 方法,并不是对直接黑塞矩阵优化的认可。黑塞矩阵向量积可以通过嵌套条带有效计算,这也是一种更有效的二阶优化方法。
x = tf.random.normal([7, 5])
layer1 = tf.keras.layers.Dense(8, activation=tf.nn.relu)
layer2 = tf.keras.layers.Dense(6, activation=tf.nn.relu)
with tf.GradientTape() as t2:
with tf.GradientTape() as t1:
x = layer1(x)
x = layer2(x)
loss = tf.reduce_mean(x**2)
g = t1.gradient(loss, layer1.kernel)
h = t2.jacobian(g, layer1.kernel)
print(f'layer.kernel.shape: {layer1.kernel.shape}')
print(f'h.shape: {h.shape}')
layer.kernel.shape: (5, 8)
h.shape: (5, 8, 5, 8)
要将此黑塞矩阵用于牛顿方法步骤,首先需要将其轴展平为矩阵,然后将梯度展平为向量:
n_params = tf.reduce_prod(layer1.kernel.shape)
g_vec = tf.reshape(g, [n_params, 1])
h_mat = tf.reshape(h, [n_params, n_params])
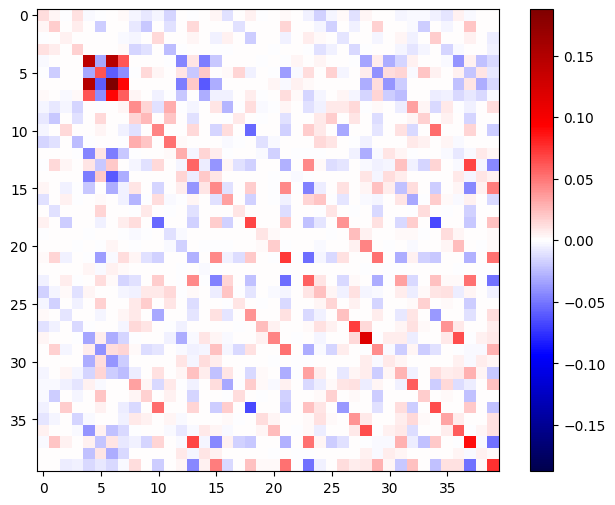
黑塞矩阵应当对称:
def imshow_zero_center(image, **kwargs):
lim = tf.reduce_max(abs(image))
plt.imshow(image, vmin=-lim, vmax=lim, cmap='seismic', **kwargs)
plt.colorbar()
imshow_zero_center(h_mat)
牛顿方法更新步骤如下所示。
eps = 1e-3
eye_eps = tf.eye(h_mat.shape[0])*eps
注:实际上不反转矩阵。
# X(k+1) = X(k) - (∇²f(X(k)))^-1 @ ∇f(X(k))
# h_mat = ∇²f(X(k))
# g_vec = ∇f(X(k))
update = tf.linalg.solve(h_mat + eye_eps, g_vec)
# Reshape the update and apply it to the variable.
_ = layer1.kernel.assign_sub(tf.reshape(update, layer1.kernel.shape))
虽然这对于单个 tf.Variable 来说相对简单,但将其应用于非平凡模型则需要仔细的级联和切片,以产生跨多个变量的完整黑塞矩阵。
批量雅可比矩阵#
在某些情况下,您需要取各个目标堆栈相对于源堆栈的雅可比矩阵,其中每个目标-源对的雅可比矩阵都是独立的。
例如,此处的输入 x 形状为 (batch, ins) ,输出 y 形状为 (batch, outs):
x = tf.random.normal([7, 5])
layer1 = tf.keras.layers.Dense(8, activation=tf.nn.elu)
layer2 = tf.keras.layers.Dense(6, activation=tf.nn.elu)
with tf.GradientTape(persistent=True, watch_accessed_variables=False) as tape:
tape.watch(x)
y = layer1(x)
y = layer2(y)
y.shape
TensorShape([7, 6])
y 相对 x 的完整雅可比矩阵的形状为 (batch, ins, batch, outs),即使您只想要 (batch, ins, outs)。
j = tape.jacobian(y, x)
j.shape
TensorShape([7, 6, 7, 5])
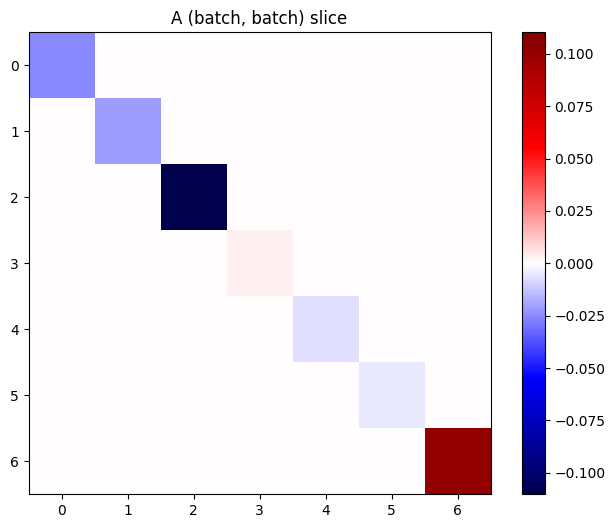
如果堆栈中各项的梯度相互独立,那么此张量的每一个 (batch, batch) 切片都是对角矩阵:
imshow_zero_center(j[:, 0, :, 0])
_ = plt.title('A (batch, batch) slice')
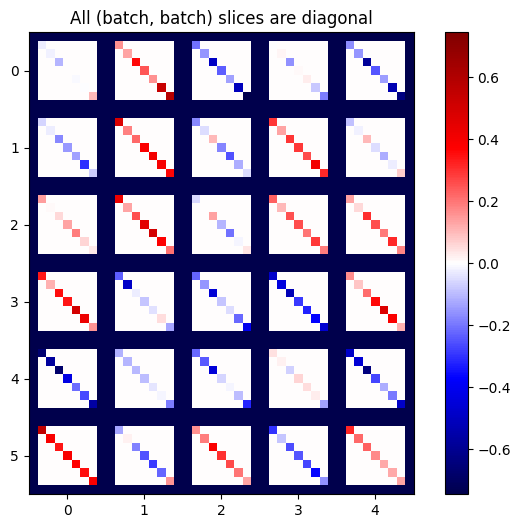
def plot_as_patches(j):
# Reorder axes so the diagonals will each form a contiguous patch.
j = tf.transpose(j, [1, 0, 3, 2])
# Pad in between each patch.
lim = tf.reduce_max(abs(j))
j = tf.pad(j, [[0, 0], [1, 1], [0, 0], [1, 1]],
constant_values=-lim)
# Reshape to form a single image.
s = j.shape
j = tf.reshape(j, [s[0]*s[1], s[2]*s[3]])
imshow_zero_center(j, extent=[-0.5, s[2]-0.5, s[0]-0.5, -0.5])
plot_as_patches(j)
_ = plt.title('All (batch, batch) slices are diagonal')
要获取所需结果,您可以对重复的 batch 维度求和,或者使用 tf.einsum 选择对角线:
j_sum = tf.reduce_sum(j, axis=2)
print(j_sum.shape)
j_select = tf.einsum('bxby->bxy', j)
print(j_select.shape)
(7, 6, 5)
(7, 6, 5)
没有额外维度时,计算会更加高效。tf.GradientTape.batch_jacobian 方法就是如此运作的:
jb = tape.batch_jacobian(y, x)
jb.shape
TensorShape([7, 6, 5])
error = tf.reduce_max(abs(jb - j_sum))
assert error < 1e-3
print(error.numpy())
0.0
小心:tf.GradientTape.batch_jacobian 只验证源和目标的第一维是否匹配,并不会检查梯度是否独立。用户需要确保仅在合理条件下使用 batch_jacobian。例如,添加 tf.keras.layers.BatchNormalization 将破坏独立性,因为它在 batch 维度进行了归一化:
x = tf.random.normal([7, 5])
layer1 = tf.keras.layers.Dense(8, activation=tf.nn.elu)
bn = tf.keras.layers.BatchNormalization()
layer2 = tf.keras.layers.Dense(6, activation=tf.nn.elu)
with tf.GradientTape(persistent=True, watch_accessed_variables=False) as tape:
tape.watch(x)
y = layer1(x)
y = bn(y, training=True)
y = layer2(y)
j = tape.jacobian(y, x)
print(f'j.shape: {j.shape}')
j.shape: (7, 6, 7, 5)
plot_as_patches(j)
_ = plt.title('These slices are not diagonal')
_ = plt.xlabel("Don't use `batch_jacobian`")
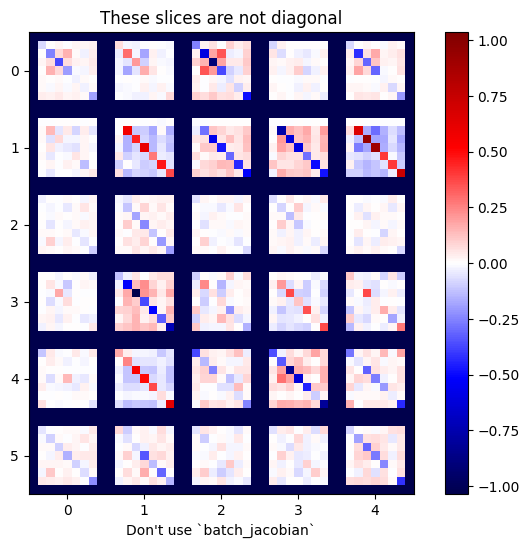
在此示例中,batch_jacobian 仍然可以运行并返回某些信息与预期形状,但其内容具有不明确的含义:
jb = tape.batch_jacobian(y, x)
print(f'jb.shape: {jb.shape}')
jb.shape: (7, 6, 5)


