定点表示法的乘法示例

参考：Multiplication Examples Using the Fixed-Point Representation

要执行定点乘法，可以首先忽略乘数和被乘数的二进制小数点，将操作数视为两个补码数字进行乘法运算，然后确定结果的二进制小数点位置。

二进制乘法的笔算方法与十进制乘法的笔算方法类似。它有两个阶段：首先生成部分积，然后将这些部分积相加得到最终结果。这实际上是基于乘法是将一个数字连续加到自己身上的思想。下面的例子 1 详细阐述了这个过程。然后，我们将讨论需要处理带符号数字的情况。

无符号数的无符号乘法

假设 \(a=101.001_2\) 和 \(b=100.010_2\) 是两个 Q3.3 格式的无符号数字。求 \(a \times b\)。

考虑到二进制小数点的位置，我们可以将 \(a\) 和 \(b\) 表示为

\[\begin{split} a=\big(101001 \big)_{2} \times \big (2^{-3} \big)_{10}\\ b=\big(100010 \big)_{2} \times \big (2^{-3} \big)_{10} \end{split}\]

则有：

\[ \begin{align}\begin{aligned}\begin{split} \begin{equation} \begin{split} a \times b &= \bigg( \big(101001 \big)_{2} \times \big (2^{-3} \big)_{10} \bigg) \times \bigg( \big(100010 \big)_{2} \times \big (2^{-3} \big)_{10} \bigg)\\ &= \bigg( \big(101001 \big)_{2} \times \big(100010 \big)_{2} \bigg) \times \big( 2^{-6} \big)_{10}\end{split}\\\end{split} \end{equation} \end{aligned}\end{align} \]

这意味着我们可以忽略 \(a\) 和 \(b\) 的二进制小数点，执行乘法运算，然后将二进制小数点放在乘积的第六位左边，以获得正确的乘法结果。因此，在这里，我们首先忽略 \(a\) 和 \(b\) 的二进制小数点。现在，为了进行乘法运算，我们必须从右到左依次选择乘数的一位数字，找到这个数字与被乘数的积以获得相应的部分积。然后，以类似于十进制乘法的方式，我们应该适当地将部分积向左移动并将它们相加在一起。

为了验证二进制乘法，我们需要给出被乘数、乘数和结果的十进制等值。橙色的数字表示将来参考的行号。现在，我们应该将二进制小数点放在乘积的第六位左边，得到 \(a \times b=10101.110010_2=21.78125_{10}\)。

结果可以比乘数和被乘数要大得多。因此，我们需要足够长的字长度来代表结果，以确保正确无误。要防止潜在的溢出，我们需要多少位来表示结果？考虑上述前两个部分积之和(第 3 行和第 4 行之和) 。在这种情况下，我们将一个六位数字 \(p1=000000_2\)与一个七位数字 \(p2=1010010_2\) 相加（注意第二个部分产品向左移动了一位）。这两个数的和，\(p1+p2\) 通常可以是一个八位数(比 \(p2\) 的长度长一)。

让我们用 \(p3\) 表示向左移动两位的第三个部分结果，即 \(p_3=00000000\)。将 \(p3\)加到 \(p1+p2\) 上，我们实际上是在将两个八位数字相加，一般情况下，结果可以是一个九位数字（比 \(p3\) 的长度长一）。继续这个过程，我们观察到结果可以比最后一个部分产品适当移位后的版本长一位。例如，上述乘法的最后一个部分产品向左移动了五位。因此，我们有 \(p_6=10100100000_2\)。这是一个 11 位数字，因此，乘积 \(a\times b\) 最多可以有 12 位。

考虑到这个例子的一般形式，你可以轻松地计算出两个数字相乘所需的字长。一般来说，如果 \(a\) 和 \(b\) 分别是长度为 \(L_a\) 和 \(L_b\) 位的数字，我们需要使用 \(L_a+L_b\) 位来表示 \(a\times b\) 以避免溢出。

小技巧

假设 \(a\) 和 \(b\) 分别为 \(Qn_1.m_1\) 和 \(Qn_2.m_2\) 格式的两个数字，则 \(a \times b\) 将是 \(Qn.m\)（\(n=n1+n2\) 且 \(m=m1+m2\)）。

二进制补码的重要特征

二进制数 \(x= \big (x_{M-1}x_{M-2} \dots x_0 \big )_2\) 的补码为

\[ x=-x_{M-1} \times 2^{M-1}+ \sum_{i=0}^{M-2}x_{i} \times 2^{i} \]

推导过程（对于负数的）：

\[\begin{split} \begin{align} \bigg( 1 \; x_{M-2}...x_{0} \bigg)_{Two's \; Complement} &=- \bigg( 2^M - \big( 1 \; x_{M-2}...x_{0} \big)_{Two} \bigg) \\ &=- 2^M + 2^{M-1} + \sum_{i=0}^{M-2}x_{i} \times 2^{i} \\ &= - 2^{M-1} + \sum_{i=0}^{M-2}x_{i} \times 2^{i} \end{align} \end{split}\]

这意味着我们可以通过将无符号数从二进制转换为十进制表示的方式来找到补码数字的等效十进制值，除了我们必须用负权重(negative weight)解释符号位。举个例子，假设 \(x=101_2\) 是一个以补码格式表示的数字。使用公式，我们有 \(x=-1 \times 2^{2} + 0 \times 2^{1} + 1 \times 2^{0} = -3\)。我们可以用更常见的方法来获得相同的结果，即找到负数的补码数字的等效十进制值。由于 \(x\) 是负数，我们有 \(x=-(011_2)=-3_{10}\).

无符号数乘以有符号数

假设两个 Q2.3 数 \(a=01.001_2\) 和 \(b=10.010_2\)（假设 \(a\) 是无符号数，但 \(b\) 是有符号数），有

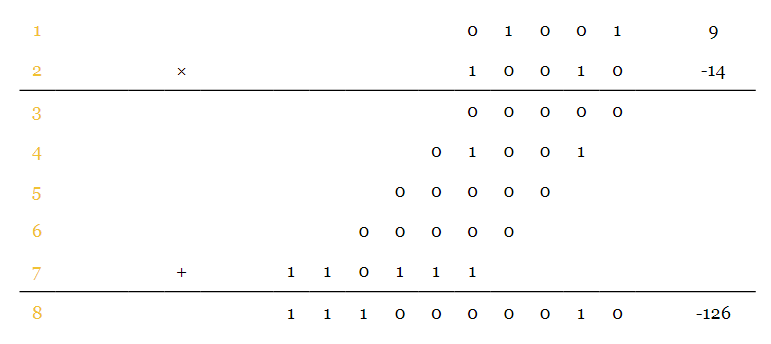
请注意最后一个部分结果（第7行）。由于乘数 \(b\) 是有符号数字，其最高有效位（most significant bit，缩写 MSB）是符号位。根据等式(3)，可以通过将该数字视为无符号数字来找到二进制补码数字的等效十进制值，但我们必须以负权重解释符号位。根据等式 3 的证明，可以通过将一个二进制补码数字视为无符号数字来找到其等效的十进制值，但我们必须以负权重解释符号位。由于二进制补码数字的这个性质，我们可以将乘数视为无符号数字来进行上述乘法运算；然而，我们必须考虑 MSB 的负权重。因此，如本例中的计算所示，通过计算a的二进制补码来获得最后结果。考虑到二进制小数点的位置，我们可以得到 \(a \times b=1110.000010_2\)。结果显然是一个有符号数字，因为我们的最后一个部分结果是有符号的。为了找到这个负数的等效十进制值，我们可以写出 \(a \times b=-(0001.111110_2)=-1.96875_{10}\)。这与十进制计算一致，即 \(-1.96875=-\tfrac{126}{64}\)。

这里，我们需要强调两点：首先，由于除了最后一个部分结果之外的所有部分都是无符号的，因此我们只需要对最后一个部分进行符号扩展。其次，在计算最后一个部分的二进制补码时，我们必须用一个更长的位来表示被乘数。例如，在上面的计算中，我们将 \(a\)视为 \(001001\)，然后找到它的二进制补码。这给了我们最后一个部分为 \(110111\)。错误的替代方案是首先找到五位 \(a\) 的二进制补码，得到 \(10111\)，然后将结果进行符号扩展，得到 \(110111\)。尽管在这个特定的例子中，这两种计算给出了相同的结果，但一般情况下并非如此。下一个例子进一步阐明了这一点。

\(a=11.001_2\)，\(b=10.010_2\)，\(a\times b\)

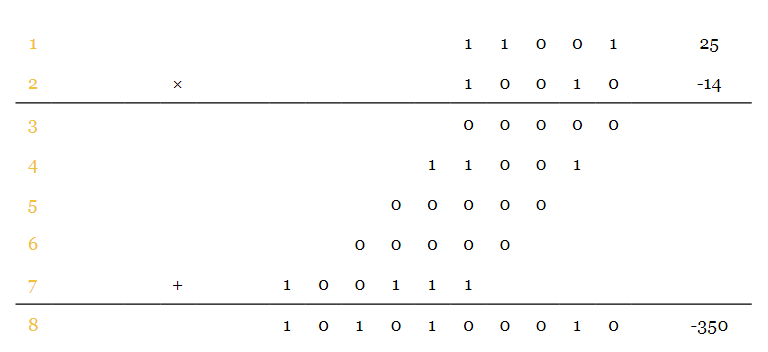
即 \(a \times b=1010.100010_2=-(0101.011110_2)=-5.46875_{10}=\tfrac{350}{64} \)。

在计算最后一个部分的二进制补码时，我们必须用一个更长的位来表示被乘数。例如，在上面的计算中，我们将 \(a\) 视为011001，然后找到它的二进制补码。这给了我们最后一个部分为 \(100111\)。这个有符号的部分是负数。我们预计这个数字会是负数，因为 \(a\) 是无符号的，但是 \(b\) 的 MSB 有一个负权重。现在，让我们检查错误的替代方案。这一次，我们首先找到五位 \(a\) 的二进制补码，得到 \(00111\)，然后将结果进行符号扩展，得到 \(000111\)。这些计算给我们一个正数，这是不正确的。总结一下，当我们计算最后一个部分产品的二进制补码时，我们必须用一个更长的位来表示被乘数，并找到它的二进制补码。

有符号数乘以有符号数