tanh 函数

对于定义域 \(\mathbb{R}\) 中的输入，tanh 函数将输入变换为区间 \((-1, 1)\) 上的输出。函数定义如下：

\[ \operatorname{tanh}(x) = \frac{1 - \exp(-2x)}{1 + \exp(-2x)}. \]

# from matplotlib import pyplot as plt
import torch
from torch_book.plotx.utils import plot

x = torch.arange(-8.0, 8.0, 0.1, requires_grad=True)
y = torch.tanh(x)
plot(x.detach(), y.detach(), 'x', 'tanh(x)', figsize=(5, 2.5))

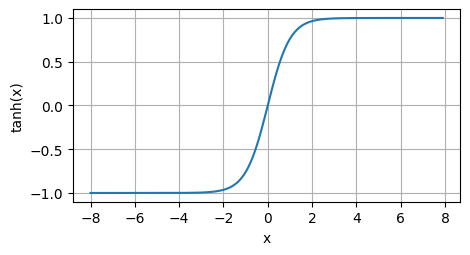
tanh 函数特性：

\[ \operatorname{tanh}(x) + \operatorname{tanh}(-x) = 0 \]

tanh 函数的导数为下面的公式：

\[ \frac{\operatorname{d}}{\operatorname{d} x} \operatorname{tanh}(x) = 1 - \operatorname{tanh}^2(x). \]

可视化导函数：

y.backward(torch.ones_like(x),retain_graph=True)
plot(x.detach(), x.grad, 'x', '$\operatorname{d} \operatorname{tanh}$', figsize=(5, 2.5))

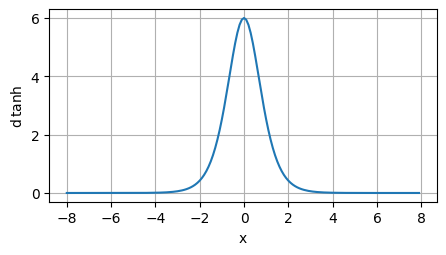
tanh 函数的泰勒展示式：

\[ \operatorname{tanh}(x) = \sum_{k=-\infty}^{\infty} \frac{x^k}{k!} \]