Coherent Semantic Attention for Image Inpainting

论文翻译：Arxiv |ICCV 2019 paper| BibTex

摘要

最新的基于深度学习的方法已为修补图像的缺失区域这一艰巨的任务显示出令人振奋的结果。然而，由于局部像素的不连续性（discontinuity），现有方法经常产生具有模糊纹理（blurry textures）和扭曲结构（distorted
structures）的内容。从语义级别的角度来看，局部像素不连续性主要是因为这些方法忽略了语义相关性（semantic relevance）和孔区域（hole regions）的特征连续性（feature continuity）。为了解决这个问题，我们研究了人类在图片修复中的行为，并提出了一种基于深度生成模型的精细方法，该方法具有新颖的连贯语义注意（coherent semantic attention，CSA）层，它不仅可以保留上下文结构，而且还能通过对孔特征之间的语义相关性进行建模，可以对缺失部分进行更有效的预测。该任务分为粗（rough）修，精（refinement）修两个步骤，我们在 U-Net 架构下使用神经网络对每个步骤进行建模，其中 CSA 层被嵌入到精修步骤的编码器（encoder）中。同时，我们进一步提出一致性损失（consistency loss）和特征补丁鉴别器（feature patch discriminator），以稳定网络训练过程并提升细节。在CelebA，Places2 和 Paris StreetView 数据集上进行的实验已验证了我们提出的方法在图像修复任务中的有效性，并且与现有的最新（state-of-the-art）方法相比，可以获得更高质量的图像（译者注：本论文源代码为：KumapowerLIU/CSA-inpainting，代码重构于 xinetzone/CSA-inpainting）。

1. 简介

图像修补是合成合理假设的缺失或损坏部分的任务，可用于许多应用程序中，例如删除不需要的物体，完成被遮挡的区域，恢复损坏或损坏的部分。图像修复的核心挑战是保持全局语义结构并为缺失的区域生成逼真的纹理细节。

传统工作 [11, 1, 4, 5, 33] 大多研究纹理合成技术来解决孔填充问题。在 [4] 中，Barnes 等人提出了 Patch-Match 算法，该算法从孔边界迭代搜索最合适的补丁，以合成缺失的内容。Wilczkowiak等 [33] 采取进一步措施并检测所需的搜索区域以找到更好的匹配补丁。但是，这些方法缺乏对高级语义的理解，并且在重建这些局部独特的模式方面遇到了困难。相反，基于早期深度卷积神经网络的方法 [16, 22, 27, 26] 学习数据分布以捕获图像的语义信息。尽管这些方法可以实现合理的修复效果，但它们无法有效地利用上下文信息来生成孔的内容，从而导致结果中包含噪声模式。

最近的一些研究有效地利用了上下文的的信息，并获得了更好的修复效果。这些方法可以分为两种类型。第一种类型 [40, 35, 30] 利用空间注意力，将周围的图像特征作为参考来恢复缺失的区域。这些方法可以确保所生成内容与上下文信息的语义一致性。但是，它们仅关注矩形孔，结果显示像素不连续且具有语义鸿沟（请参见图1(b, c)）。第二种类型 [23, 39] 是对原始图像中的有效像素进行像素丢失的条件进行预测。这些方法可以适当地处理不规则的孔，但是生成的内容仍然遇到语义错误和边界伪影（artifacts）的问题（参见图 1(g, h)）。上述方法不能很好地工作的原因是因为它们忽略了所生成内容的语义相关性和特征连续性，这对于图像级别的局部像素连续性至关重要。

为了在居中和不规则情况下获得更好的图像修复效果，我们研究了图像修复中的人的行为，发现该过程涉及概念和绘画两个步骤，以保证图像的整体结构一致性和局部像素连续性。更具体地说，一个人首先观察图像的整体结构，并在构想过程中构思出缺失部分的内容，以便可以保持图像的整体结构一致性。然后在绘画过程中将内容的想法填充到实际图像中。在绘画过程中，总是从先前绘制的线条的末端节点继续绘制新线条和着色，这实际上确保了最终结果的局部像素连续性。

受此过程的启发，我们提出了一个连贯的语义关注层（CSA），它以相似的过程填充了图像特征图的未知区域。最初，使用已知区域中最相似的特征补丁来初始化未知区域中的每个未知特征补丁。此后，通过考虑相邻补丁的空间一致性来迭代优化它们。因此，第一步可以保证全局语义的一致性，而优化步骤可以保持局部特征的一致性。

具体而言，类似于[40]，我们将图像修复分为两个步骤。第一步是通过训练一个粗糙的网络来草拟丢失的内容而构建的。在编码器中具有 CSA 层的精修网络指导第二步以精修粗略的预测。为了使网络训练过程更加稳定并激励 CSA 层更好地工作，我们提出了一致性损失，不仅可以测量 VGG 特征层与 CSA 层之间的距离，还可以测量 VGG 特征层与解码器中 CSA 的对应层。同时，除了补丁识别器[17]，我们通过引入特征补丁识别器（feature
patch discriminator）改善了细节，该特征补丁识别器比常规的识别器更易于编写，更快和更稳定[25]。除了一致性损失外，重建损失和相对论平均 LS 对抗损失[20]被作为约束条件来指导我们的模型学习有意义的参数。

我们对标准数据集 CelebA[24]，Places2[43] 和 Paris StreetView[8] 进行实验。定性和定量测试均表明，我们的方法可以产生比现有方法更高质量的修复结果。（见图 1(d, i)）。

我们的贡献总结如下：

• 我们提出了一种新颖的，连贯的语义关注层，以构造孔区域的深层特征之间的相关性。无论未知区域是不规则区域还是居中区域，我们的算法都可以实现 state-of-the-art 的修复效果。
• 为了提高 CSA 层的性能并确保训练的稳定性，我们引入一致性损失来指导 CSA 层和相应的解码器层学习 ground truth 的 VGG 特征。同时，设计并结合了特征补丁识别器，以实现更好的预测。
• 与 [40, 35, 23, 39] 相比，我们的方法可获得更高质量的结果，并生成更连贯的纹理。此外，即使修复任务分两个阶段完成，我们的整个网络也可以以端到端的方式进行训练。

2. 相关工作

2.1. Image inpainting

在文献中，以前的图像修复研究通常可以分为两类：非学习修复（Non-learning inpainting）方法和学习修复（Learning inpainting）方法。前者是具有低级功能的传统基于扩散（diffusion-based）的方法或基于补丁（diffusion-based）的方法。后者学习图像的语义以完成修复任务，并训练深度卷积神经网络来推断缺失区域的内容。

非学习方法，例如 [11, 1, 3, 5, 6, 9, 15, 2, 32, 18, 34, 28, 12, 29] 通过传播邻近信息或从类似的背景补丁复制信息来填充缺失的区域。黄等[14] 将已知区域混合到目标区域中，以最大程度地减少不连续性。但是，搜索最匹配的已知区域是非常昂贵的操作。为了应对这一挑战，Barnes 等人[4] 提出了一种快速最近邻域算法，该算法促进了图像修复应用的发展。尽管非学习方法对于表面纹理合成非常有效，但它们无法生成语义上有意义的内容，并且不适合处理较大的缺失区域。

学习方法 [38, 22, 31, 37, 41, 7, 42] 通常使用深度学习和 GAN 策略来生成孔的像素。Context encoders[26]首先训练用于图像修补任务的深度神经网络，将对抗性训练[13]引入一种新颖的编码器-解码器管道，并输出缺失区域的预测。但是，它在生成精细细节纹理方面表现不佳。此后不久，Iizuka 等人[16]扩展这项工作并提出
局部和全局区分符，以改善修复效果。然而，这需要先前的处理步骤来在孔边界附近增强颜色连贯性。杨等[36]将上下文编码器[26]的结果作为输入，并逐渐增加纹理细节以获得高分辨率的预测。但是这种方法由于其优化过程而大大增加了计算成本。刘等 [23]更新每一层中的遮罩，并使用遮罩值重新标准化卷积权重，这确保了卷积滤波器将注意力集中在来自已知区域的有效信息上，以处理不规则的孔。Yu等[39]进一步建议使用门控卷积自动学习掩码，并与 SN-PatchGAN 鉴别器结合以实现更好的预测。但是，这些方法未明确考虑有效特征之间的相关性，因此会导致完整图像出现色差或不一致。

2.2. Attention based image inpainting

近来，基于上下文和孔区域之间的关系的空间注意力通常用于图像修复任务。上下文注意力[40]提出了一个上下文注意力层，该层搜索与粗略预测具有最高相似性的背景补丁集合。严等人[35]介绍了一种由 移位操作（shift operation）和引导损失（guidance loss）驱动的 shift-net。移位操作推测编码器层中的上下文区域与解码器层中的关联孔区域之间的关系。宋等[30]介绍了一个补丁交换（patch-swap）层，它用上下文区域中最相似的补丁替换了特征图缺失区域内的每个补丁，并通过 VGG 网络提取了特征图。尽管[40]具有通过注意分数的融合来促进空间连贯性的空间传播层，但它无法对孔区域内部面片之间的相关性进行建模，这也是其他两种方法的缺点。为此，我们提出了解决此问题并取得更好结果的方法，这在第3节中进行了详细介绍。

3.方法

我们的模型包括两个步骤：粗糙修补和细化修补。如[40]中所述，这种体系结构有助于稳定训练并扩大感受野（receptive fields）范围。我们的修复系统的总体框架如图2所示。令 $I_{gt}$ 表示 ground truth 图像，$I_{in}$ 作为对粗略网络的输入。我们首先在粗糙的修复过程中获得了粗糙的预测 $I_p$。然后，带有 CSA 层的细化网络将 $I_p$ 和 $I_{in}$ 作为输入对，以输出最终结果 $I_r$。最后，patch 和特征 patch 判别器共同协作，以获得更高的分辨率 $I_r$。

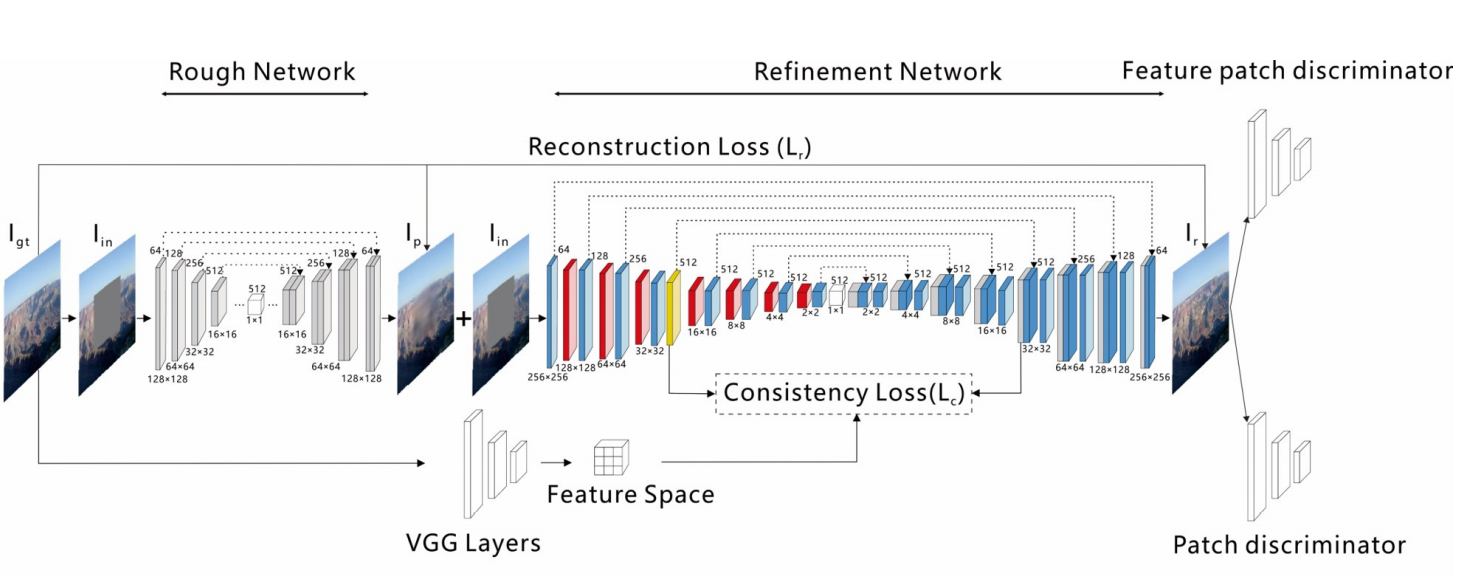
3.1 Rough inpainting

粗略网络 $I_{in}$ 的输入是具有中心或不规则孔的 $3 \times 256 \times 256$ 图像，该图像被发送到粗略网络以输出粗略预测 $I_p$。我们的粗糙网络的结构与[17]中的生成网络相同，它由 $4\times 4$ 卷积和跳跃连接组成，以将来自编码器每一层和对应解码器层的特征连接起来。粗略网络经过明确的 $L_1$ 重建损失训练。

3.2. Refinement inpainting

3.2.1 refinement network

我们使用以 $I_{in}$ 为条件的 $I_p$ 作为预测最终结果 $I_r$ 的细化网络的输入。这种类型的输入会堆叠已知区域的信息，以敦促网络更快地捕获有效特征，这对于重建孔区域的内容至关重要。细化网络由编码器和解码器组成，其中类似于粗糙网络，也采用跳跃连接。在编码器中，每个层都由 $3\times 3$ 卷积和 $4\times 4$ 空洞卷积组成。$3\times 3$ 卷积保持相同的空间大小，同时通道数量加倍。这种大小的层可以提高获取深度语义信息的能力。$4\times 4$ 空洞卷积将空间大小减小一半，并保持相同的通道数。空洞卷积可以扩大感受野，从而可以防止过多的信息丢失。CSA 层嵌入在编码器的第四层中。解码器的结构与没有 CSA 层的编码器对称，并且所有 $4\times 4$ 卷积都是反卷积（deconvolution）。

3.2.2 Coherent Semantic Attention

我们认为，仅考虑特征图中 $M$ 与 $\overline{M}$ 的关系来重建 $M$ 类似于 [40, 35, 30] 是不够的，因为忽略了生成 patch之间的相关性，这可能导致缺乏延展性以及最终结果中像素的连续性。

为了克服此限制，我们考虑了生成补丁之间的相关性，并提出了 CSA 层。我们以居中漏洞为例：CSA 层分两个阶段实施：搜索和生成。图3 说明了 CSA 层的操作，其中 $M$ 与 $\overline{M}$ 分别表示特征图中的缺失区域和已知区域。对于 $M(i \in [1,n])$（其中 $n$ 是补丁的个数）中的每个 $(1 \times 1)$ 生成补丁（generated patch）$m_i$，CSA 层在已知区域 $M$ 搜索最匹配的上下文补丁 $\overline{m_i}$ 以在搜索过程中初始化 $m_i$。然后，我们将 $\overline{m_i}$ 设置为主要部分，并将之前生成的所有补丁 $(m_{1} \cdots m_{i-1})$ 设置为次要部分，以在生成过程中恢复 $m_i$。为了测量两个部分的权重，采用了以下互相关度量：

$$D_{max_i} = \frac{\langle m_i,\overline{m_i} \rangle}{\lVert m_i \rVert \lVert \overline{m_i} \rVert} \tag{1}$$

$$D_{ad_i} = \frac{\langle m_i, m_{i-1} \rangle}{\lVert m_i \rVert \lVert m_{i-1} \rVert} \tag{2}$$

其中 $D_{max_i}$ 代表 $m_i$ 和上下文区域中最相似的补丁 $\overline{m_i}$ 之间的相似性， $D_{ad_i}$ 表示两个相邻生成的补丁之间的相似性。将 $D_{max_i}$ 和 $D_{ad_i}$ 分别归一化为上下文补丁的一部分和所有先前生成的补丁的一部分的权重。接下来，我们将详细描述这两个步骤。

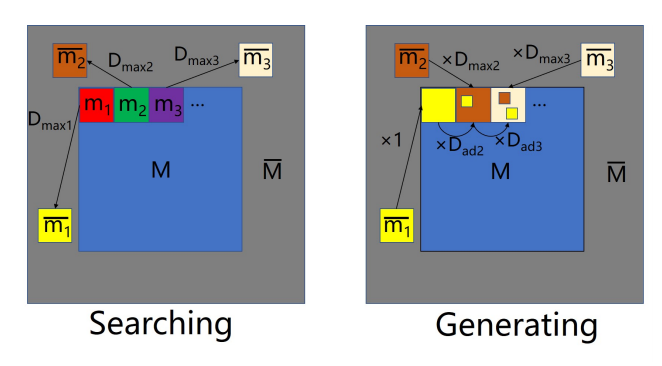
首先，我们在孔 $M$ 中搜索每个生成的补丁 $m_i$ 中最相似的上下文补丁 $\overline{m_i}$，并使用 $\overline{m_i}$ 初始化 $m_i$。然后，将先前生成的补丁和最相似的上下文补丁合并以生成当前补丁。

Searching：我首先从 $\overline{M}$ 中提取出 Patch，并且 reshape 他们为卷积核大小，然后在 $M$ 上进行卷积。通过此操作，我们可以获得一个值向量，该值表示 $M$ 中的每个补丁与 $\overline{M}$ 中的所有补丁之间的互相关。在此基础上，对于每个生成的补丁 $m_i$，我们使用最相似的上下文补丁 $\overline{m_i}$ 对其进行初始化，并为下一个操作为其分配最大互相关值 $D_{max_i}$。Generating：$M$ 的左上方补丁被用作生成过程的初始补丁（在图3中用 $m_1$ 标记）。由于 $m_1$ 没有先前的补丁，因此 $D_{ad_1}$ 为 $0$，我们直接将 $m_1$ 替换为 $\overline{m_1}$，即 $m_1 = \overline{m_1}$。虽然下一个补丁 $m_2$ 具有先前的补丁 $m-1$ 作为附加参考，但是我们因此将 $m_1$ 视为卷积滤波器，以测量 $m_1$ 与 $m_2$ 之间的互相关度量 $D_{ad_2}$。然后，将 $D_{ad_2}$ 和 $D_{max_2}$ 合并并归一化分别为 $m_1$ 和 $\overline{m_2}$ 的权重，以生成 $m_2$ 的新值，$$m_2 =\frac{D_{ad_2}}{D_{ad_2} + D_{max_2}} \times m_1 + \frac{D_{max_2}}{D_{ad_2} + D_{max_2}} \times \overline{m_2}$$。总而言之，从 $m_1$ 到 $m_n$，生成过程可以总结为：

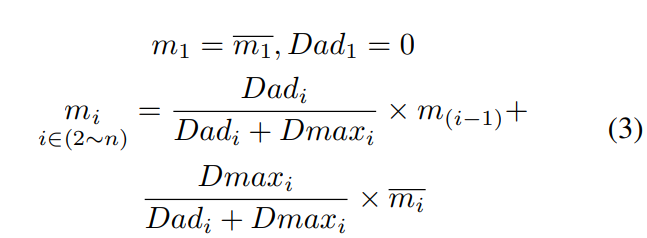
如等式3 所示，生成操作是一个迭代过程，每个 $m_i$ 都包含 $\overline{m_i}$ 和 $(m_1 \cdots m_{i-1})$ 的信息，当我们计算 $m_i$ 和 $m_{i-1}$之间的 $D_{adi_}$ 时，$m_i$ 和 $(m_1 \cdots m_{i-1})$ 之间的相关性被全部考虑。并且由于 $D_{adi_}$ 值的范围是 $0$ 到 $1$，因此当前生成的补丁和先前生成的补丁之间的相关性随着距离的增加而减小。基于等式3，我们得到一个注意图 $A_i$，它针对 $m_i$ 记录了 $\frac{D_{max_i}}{D_{adi_}+D_{max_i}}$ 和 $\frac{D_{ad_i}}{D_{adi_}+D_{max_i}} \times A_{i-1}$，然后从 $A_1$ 到 $A_n$ 形成注意力矩阵，最后将 $\overline{M}$ 中提取的色块重新用作反卷积滤波器以重建 $M$。算法1 中显示了 CSA 层的过程。

为了解释 CSA 层，我们在图4 中可视化了一个像素的注意力图，其中红色正方形标记了像素的位置，背景是我们修复的结果，深红色表示较大的关注值，浅蓝色表示较小的注意值。

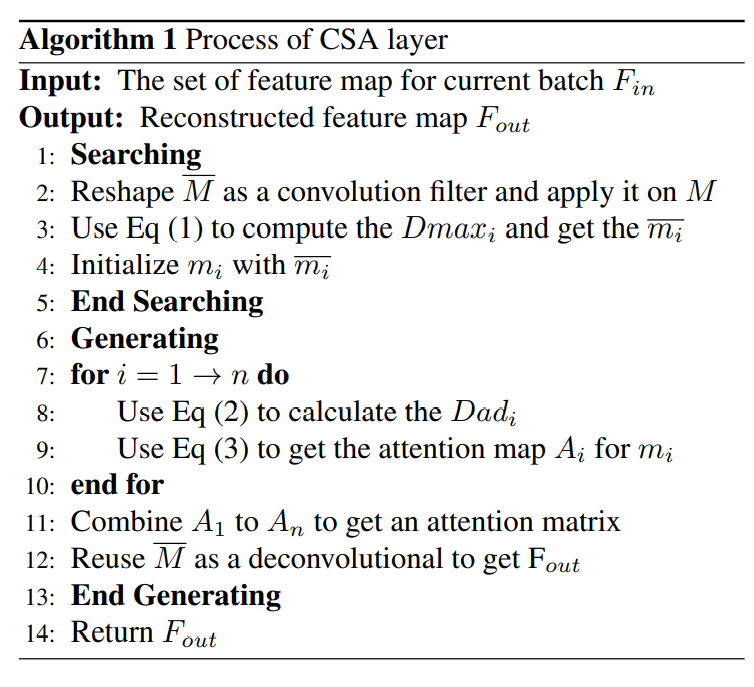
3.3. Consistency loss

一些方法[27, 23]使用感知损失（perceptual loss）[19]来提高网络的识别能力。但是，感知损失不能直接优化指定的卷积层，这可能会误导 CSA 层的训练过程。此外，感知损失不能确保 CSA 层之后的特征图与解码器中相应层之间的一致性。

然后，我们重新设计感知损失的形式，并提出一致性损失来解决此问题。如图2所示，我们使用 ImageNet 预训练的 VGG-16 提取原始图像中的高级特征空间。接下来，对于 $M$ 中的任何位置，我们将特征空间分别设置为解码器中 CSA 层和 CSA 对应层的目标，以计算 $L_2$ 距离。为了匹配特征图的形状，我们采用 VGG-16 的 4_3 层作为一致性损失。一致性损失定义为：

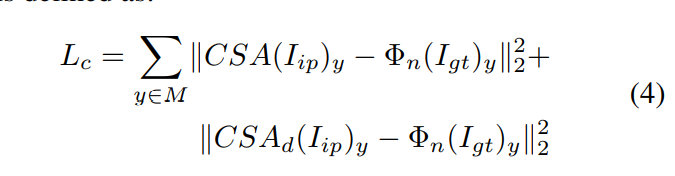
其中 $\Phi_n$ 是 VGG-16 中选定层的激活图。$CSA(.)$ 表示 CSA 层之后的特征，$CSA_d(.)$ 是解码器中的相应特征。指导损失类似于我们在[35]中提出的一致性损失。他们将缺少零件的真实编码器特征视为稳定训练的指导。然而，通过移位网提取 ground true 特征是一项昂贵的操作，并且移位网的语义理解能力不如 VGG 网络。而且，它不能同时优化编码器和解码器的特定卷积层。总而言之，我们的一致性损失更适合我们的要求。

3.4. Feature Patch Discriminator

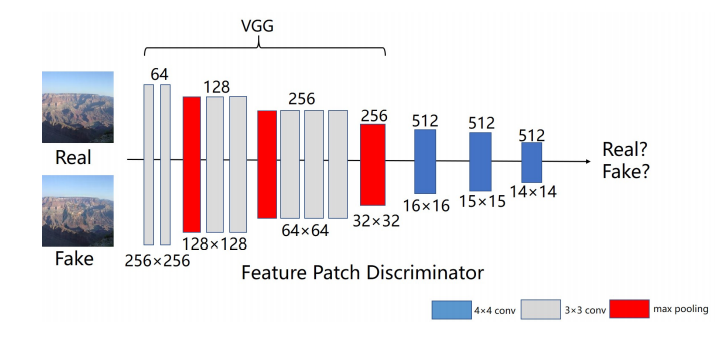
先前的图像修复网络始终使用其他本地鉴别器来改善结果。但是，局部鉴别器不适用于不规则的孔，该孔可以具有任何形状和任何位置。由 Gated Conv[39]，Markovian Gans[21] 和 SRFeat[25]推动，我们开发了一种特征补丁识别器，通过检查特征图来区分完整图像和原始图像。如图5所示，我们使用 VGG-16 在 pool3 层之后提取特征图，然后将该特征图作为几个下采样层的输入以捕获 Markovain 补丁的特征统计信息[21]。最终，我们直接在此特征图中计算对抗损失，因为此特征图中每个点的接受域仍可以覆盖整个输入图像。我们的特征补丁鉴别器结合了传统特征鉴别器[25]和补丁鉴别器[17]的优点，不仅在训练过程中快速稳定，而且使精炼网络合成了更有意义的高频细节。

除了特征色块鉴别器外，我们使用 $70\times 70$ 色块鉴别器通过类似于[25]的检查其像素值来区分 $I_r$ 和 $I_{gt}$ 图像。同时，我们使用相对论平均LS对抗损失[20]作为判别器。这种损失可以帮助精炼网络从对抗训练中生成的数据和实际数据的梯度中受益，这对于训练的稳定性是有利的。细化网络的 GAN 损耗项 $D_R$ 和鉴别器的损耗函数 $D_F$ 定义为：

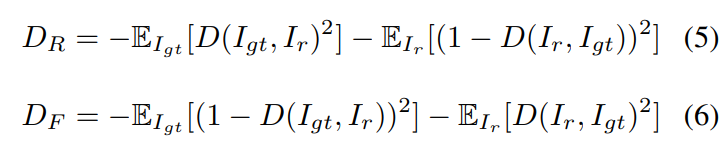
其中 $D$ 代表鉴别符，$\mathbb{E}[.]$ 代表对小批处理中所有 real/fake 数据取平均值的操作。

3.5. Objective

按照[35]，我们使用 $L_1$ 距离作为重构损失，以保证约束 $I_p$ 和 $I_r$ 应该近似于真实图像：

$$L_{re} = \lVert I_p - I_{gt} \rVert_1 + \lVert I_r - I_{gt} \rVert_1 \tag{7}$$

考虑到一致性，对抗性和重建损失，我们的优化网络和粗糙网络的总体目标定义为：

$$L = \lambda_r L_{re} +\lambda_c L_c + \lambda_d D_R \tag{8}$$

其中$\lambda_r, \lambda_c, \lambda_d$ 分别是重构，一致性和对抗性损失的权衡参数。

训练参数

• $lr=2e-4$
• $\beta_1 = 0.5$
• $\lambda_r = 1$
• $\lambda_c = 0.01$
• $\lambda_d = 0.002$